牛頓328,，導(dǎo)數(shù)是縱坐標(biāo)微分dy除以橫坐標(biāo)微分dx,，所以導(dǎo)數(shù)也叫微信商。

微分到底是什么意思,？有什么實際意義,？-用戶提問

...微分,，微分和微分:見牛頓321 ~ 327...

...意義，義和意義:見歐幾里德26...

(…歐幾里德:小說的標(biāo)題…)

湖亭觀雪(2018 . 1 . 25編輯,，2599人贊同答案):

…

好了,，最后做個總結(jié):

...概要:參見歐幾里德86...

(1)經(jīng)典微分學(xué)(見牛頓325)和極限微分學(xué)(見牛頓326)的本質(zhì)區(qū)別在于，前者體系中,，微分是變化本身,，后者體系中,，微分是變化的近似。

...本質(zhì),，質(zhì)量和本質(zhì):見歐幾里德22...

...身體,，系統(tǒng)和系統(tǒng):見歐幾里德27...

...變化，變化,，變化:見伽利略10...

(……伽利略:小說的標(biāo)題……)

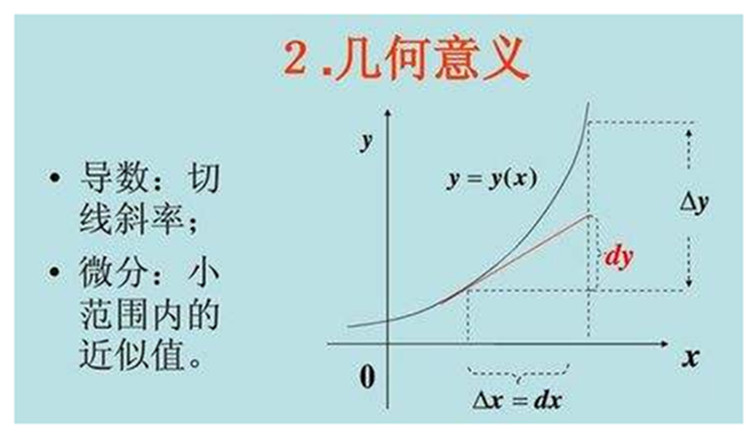
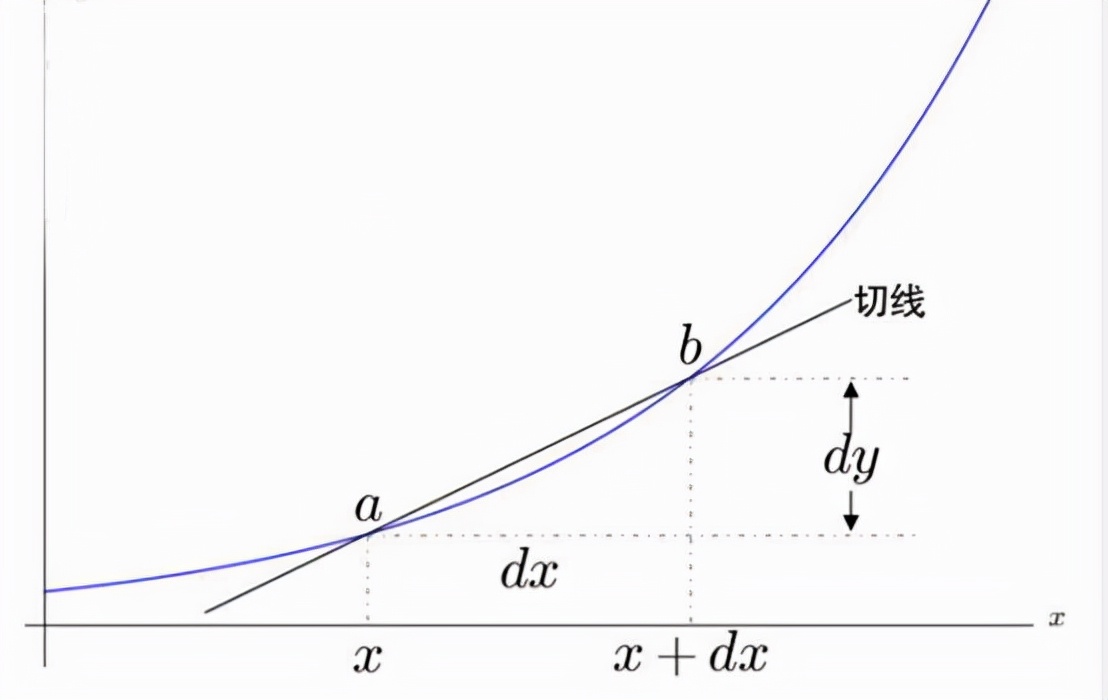
（2）微分是實實在在的一個量,，是一個無窮小量（當(dāng)變化趨近于0時）。它也是有自己的運算法則的,，參見高等數(shù)學(xué)教材,。其實跟導(dǎo)數(shù)的規(guī)則差不多。(2)微分是一個實量,，也是一個無窮小量(變化趨近于0時)。它也有自己的算法,，見高等數(shù)學(xué)教材,。其實和求導(dǎo)法則差不多。

...一無所有,，貧窮,，無限，小,，無窮小,，數(shù)量，無窮小:參見牛頓280...

...運算,，計算,，操作:參見歐幾里得121...

...法律，原則和法律:見歐幾里德108...

...導(dǎo)數(shù),、數(shù)和導(dǎo)數(shù):參見牛頓288 ~ 294...

...規(guī)則,，原則和規(guī)則:見牛頓75...

(3)我們現(xiàn)在學(xué)習(xí)的系統(tǒng)是按照先極限，再通過極限定義導(dǎo)數(shù),，再通過導(dǎo)數(shù)定義微分的順序來的,。

...身體，系統(tǒng)和系統(tǒng):見歐幾里德27...

...極限,，極限,，極限:參見歐幾里得202 ~ 321...

...定義，意義和定義:見歐幾里德28...

但在歷史發(fā)展中,，先定義微分(即先定義dy),，再根據(jù)需要定義導(dǎo)數(shù)(解決切線問題)。

...日歷,，歷史,，歷史:見歐幾里得111...

...發(fā)展,，展覽和發(fā)展:見伽利略21...

...d:差異首字母...

【微分(英語):n .(名詞)差；差異,；價格差異,；工資等級(尤指同一行業(yè)不同工作的)。

(形容詞)不同,；視差異而定,；這是有區(qū)別的。

-牛頓321

dx是什么意思,？,？-用戶提問

2019 . 9 . 7想玩一個游戲的貓:d(x)代表區(qū)分x。

dy/dx中的d表示“微增量”,，即微增量y除以微增量x,，在函數(shù)中表示微分。

Dx是X的微分,，是增量的細(xì)化,。dx是一個非常非常小的x。

——《牛頓3》]

...切線,、直線和切線:參見牛頓288...

(4)至于為什么要定義微分,？我相信如果你以后接觸到數(shù)學(xué)領(lǐng)域更高級的知識，你就會明白為什么微分一定要定義,。

...知識,，知識，知識:見歐幾里德5,，6...

(5)微分是微分,，導(dǎo)數(shù)是導(dǎo)數(shù)。

不要因為某些歷史巧合(見牛頓327)(比如切點),，就按照自己想象的規(guī)律瞎折騰,。

...日歷，歷史,，歷史:見歐幾里得111...

...猜想,，猜想:參見牛頓221...

...規(guī)則，原則和規(guī)則:見牛頓75...

不懂的時候,，多想想極限的思想,。

...思考，思考,，思考:參見歐幾里得154...

第四,，導(dǎo)數(shù)和微分的區(qū)別

最后，我們來談?wù)剬?dǎo)數(shù)和微分的區(qū)別:

導(dǎo)數(shù):指函數(shù)在某一點變化的速度,，是變化率,。

...函數(shù),，數(shù)字和函數(shù):參見歐幾里德52...

...變化，變化,，變化:見伽利略10...

...率:見歐幾里得58...

微分:指函數(shù)在某一點的變化量(趨近無窮小),，是一個變量。

評論:

吳登2020-06-02

如果你能理解導(dǎo)數(shù),，你就能理解微分,。導(dǎo)數(shù)是縱坐標(biāo)的微分(y切n，n→無窮大)除以橫坐標(biāo)的微分(x切n,，n→無窮大),，所以導(dǎo)數(shù)也叫微信業(yè)務(wù)。

“一個復(fù)變函數(shù),，自變量有微小的變化,，比如0.003，函數(shù)的變化是多少,，也就是函數(shù)的微分,。

請看牛頓329下集，微分的實際意義:計算復(fù)變函數(shù)的微小變化,。

不了解歷史，就看不清未來,。

歡迎來到頭條“人性的游戲”